Hardcover, 2011, ISBN 978-0-19-533667-2, 450 pages with illustrations, index, bibliographic references, and online examples, US $39.95; available from Oxford University Press, 198 Madison Avenue, New York, New York 10016, USA; telephone (+1) 212-726-6000; http://www.oup.com; online examples and supporting material: http://www.oup.com/us/companion.websites/9780195336672/examples/?view=usa/.

Reviewed by Michael Gogins
New York, New York, USA

I believe A Geometry of Music (hereinafter AGM) is a ground-breaking book in music theory. According to Dmitri Tymoczko, “While my stated audience consists of composers and music theorists, I have tried to write in a way that is accessible to students and dedicated amateurs.” If my own experience is any guide, AGM will be especially useful to composers who, like myself, use computers in composition. Indeed, this review is written mainly from the viewpoint of an algorithmic composer. But, as much as my informal education in music theory permits, I will also attempt to give the book some historical and theoretical context.

AGM synthesizes about 15 years of work by the author (and some other theorists) towards developing a geometric understanding of many phenomena in voice leading, chord structure, chord progression, scale theory, and modulation. The starting point is to define each chord as a single point in a continuous Euclidean “chord space” with as many dimensions of pitch as the chord has voices. This simple idea turns out to be tremendously fruitful. Tymoczko convincingly argues that all commonly used measures of voice-leading distance agree with the length of the distance from one chord point to another chord point in chord space.

AGM proposes that music which is tonal in the broadest meaning of the term, from the beginnings of Western polyphony until the extended tonality of today, and across many different classical and popular styles, features conjunct melodic motion, acoustic consonance, harmonic consistency, limited macroharmony (the notion of scale, more or less), and centricity (having a tonal center in the standard sense). I suspect that for academic theorists, the main interest of AGM will be its use of the geometric definition of voice-leading distance to develop a deeper understanding of these phenomena.

According to Tymoczko’s theory, a chord is a point, and voice-leading is movement from one point to another point. Of course, music theorists use many different levels of abstraction in thinking about chords and scales. Theorists almost always abstract from the order of the voices, they usually ignore the particular octave of a pitch, and sometimes even ignore the particular inversion of a chord. And they generally ignore voice doublings. AGM shows that each of these levels of abstraction exactly corresponds to what mathematicians call an “equivalence class” in chord space. For example, the standard definition of a “pitch-class set” corresponds to combining the equivalence classes for octave (“O”), order of voices (“P” for permutation), and number of voices (“C” for cardinality): OPC. Other equivalence classes are “T” (for translational equivalence, i.e., OPTC equivalent chords are the same chord type) and “I” (for inversional equivalence).
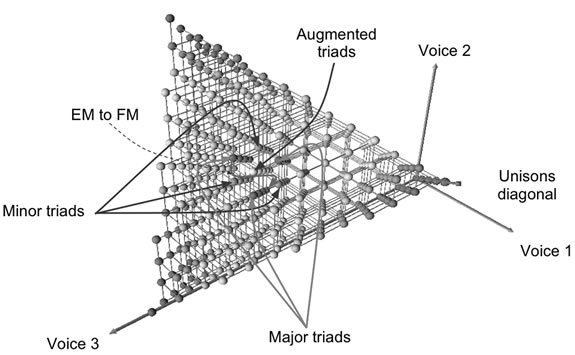
When an equivalence class, or combination of classes, is imposed upon a space, then all points that are the same with respect to the equivalence class become “glued together.” The space thus becomes a “quotient space” or “orbifold.” For example, the chord space for trichords under OPC equivalence becomes a tilted prism whose equilateral faces are glued together modulo a one-third twist (Orbifold for trichords). The chord points in twelve-tone equal temperament are colored balls. The lines connecting the chords are the semitone voice-leadings. The four augmented triads run up the center of this prism; the twelve major and twelve minor triads surround the augmented triads in six alternating columns of four chords, each glued together to form a twisted torus. The two-pitch trichords are on the sides of the prism, and the one-pitch or unison trichords are on the edges of the prism. Transposition equates to moving a chord in parallel with the diagonal of unisons in chord space. When a chord reaches the end face of this orbifold it re-appears with a one-third twist on the opposite end face (in the figure, this is shown in the movement from E major to F major). Inversion equates to reflecting across the middle of the prism. Change of chord type equates to moving along the plane perpendicular to the diagonal of unisons. Chords that move in this fashion reflect off the sides of the prism. And so on. Furthermore, these concepts, based as they are on a continuous manifold, generalize to tuning systems other than twelve-tone equal temperament, and to chords of any number of voices.

Tymoczko shows that the various chord spaces derived from each equivalence class, or combination of equivalence classes, inherit a “metric” or measure of distance from their parent, in purely Euclidean chord space. This is the signal fact that enables the concept of voice-leading distance to be used in more or less the same way with respect to pitch-class sets (OPC equivalence), chord types (OPTC equivalence), and set-classes (OPTIC equivalence). AGM further demonstrates that the concept of voice-leading, and of minimal voice-leading operations, applies not only to chords and chord progressions but, just as well, to scales and modulations. Indeed, Tymoczko argues, the use of the same measure of voice-leading distance for both chord progression and modulation provides a geometric foundation for understanding something many musicians feel: that there is a kind of self-similarity between chord progressions in the small scale and modulations in the medium-to-large scale.

AGM goes on to discuss atonal music, chromatic harmony, the structure of typical and normative chord progressions, modern and contemporary uses of variant scales, and many other matters using the underlying geometry of chord space with its measure of voice-leading distance as the unifying principle. Additionally, AGM draws on examples beginning with the two-voice counterpoint of the Middle Ages and ending with the extended tonality of Dmitri Shostakovitch, Bill Evans, and Steve Reich. Audio clips of these examples are accessible to the public on the Web site accompanying the book listed above. These online recordings and score excerpts greatly increase the usefulness of the book. Readers with keyboard skills would benefit from playing through the examples. Readers without such skills would benefit from careful listening to the online audio clips while following the score excerpts.

This book is a further step along the path that began when Pythagoras identified musical intervals with numerical ratios, has passed through stages of increasing mathematical sophistication with the Tonnetz of Leonhard Euler and Arthur von Oettingen and the voice-leading operations of Hugo Riemann, and is now leading to something of an efflorescence of atonal set theory, group theory, neo-Riemannian theory, and geometry. Where set theorists such as Milton Babbitt (“Some Aspects of Twelve-Tone Composition”, The Score and IMA Magazine 12, 1955), Allen Forte (The Structure of Atonal Music, Yale University Press, 1973) and their school focus on combinatorics and group theory applied to a discrete representation of pitch, Tymoczko (like some contemporary transformational or neo-Riemannian theorists; see below) takes a mathematical step back to use a wider range of abstract algebra and geometry applied to a continuous representation of pitch. Furthermore, AGM demonstrates that some of the central phenomena of tonality, such as the “faithfulness” of the circle of fifths in reflecting relationships that obtain in higher-dimensional chord spaces, cannot be adequately understood without a continuous representation of pitch. I believe this alone suffices to establish the theoretical importance of the book.
The main contemporary scholars who have written books proposing a unifying mathematical framework for music theory are Tymoczko (using geometry) and Guerino Mazzola (using category theory in The Topos of Music, Birkhaüser, 2002). Perhaps Fred Lerdahl (Tonal Pitch Space, Oxford University Press, 2001) should also be mentioned. And there are others. I do not have the background in music theory to allow me to comprehensively compare these authors, or to render a final judgment on how important AGM is, or how it stacks up against, or fits together, with competing approaches. The fact that Tymoczko analyzes many of the same well-known excerpts (such as the prelude from Wagner’s Tristan und Isolde) as do other theorists should make this kind of comparison easier. But it is perhaps worth noting that almost all of the articles on music theory as such that have been published to date in Science magazine present the basic ideas of geometric music theory (overview by Julian Hook, “Exploring Musical Space,” Science 313, 2006; “The Geometry of Musical Chords,” Dmitri Tymoczko, Science 313, 2006; overview by Rachel Wells Hall, “Geometrical Music Theory,” Science 320, 2008; Clifton Callender, Ian Quinn, and Dmitri Tymoczko, “Generalized Voice-Leading Spaces,” Science 320, 2008).

One of the things AGM is trying to do is to provide a simpler view of music theory, based on principles rather than lists of rules and exceptions. The book certainly does this for me. Matters I formerly found more or less opaque, such as how those German and French sixths really work, or why some key changes are more common than others, or how tritone substitutions fit in, are now far clearer. So for me, the unification Tymoczko is attempting has in some part been achieved.

Another thing that distinguishes AGM from much writing on music theory I have seen is its ambition towards, and occasional achievement of, empiricism: comparison with data, in this case analyses of all the Mozart piano sonatas and some 70 Bach chorales. I do not think music theory must be empirical to be interesting or valid, but I do think more experimentation in music theory can bring about innovation.
AGM certainly has gaps. Perhaps it is better to say the book has a certain thinness of context. For example, AGM presents two simple graphs that concisely encapsulate the rules for well-formed chord progressions in functional harmony (and tests these graphs against the aforementioned works by Bach and Mozart). Yet I don’t find a convincing explanation of why a “harmonic cycle” goes from the tonic up a fifth to the dominant and down a fifth to the tonic again, instead of down a fifth to the subdominant and up a fifth to the tonic again. Such an explanation could be constructed from the simple fact that the perfect fifth is more consonant than the perfect fourth. More likely, perhaps, AGM just takes this for granted. But, I wonder if this specific directedness of chord progressions should be a sixth major feature of tonality. In his discussion of functional harmony, Tymoczko does provide some context by engaging in something of a polemic against the more radical members of the school of Heinrich Schenker, arguing that the attempt to generate all well-formed chord progressions, and only them, from purely contrapuntal or voice-leading considerations does not succeed. But then there is a curious lack of discussion of the transformational or neo-Riemannian approach to music theory originating with David Lewin (Generalized Musical Intervals and Transformations, Yale University Press, 1987) and carried on today by such theorists as Adrian Childs (“Moving Beyond Neo-Riemannian Triads: Exploring a Transformational Model for Seventh Chords,” Journal of Music Theory 42, 1998), Thomas Fiore and Ramon Satyendra (“Generalized Contextual Groups,” Music Theory Online 11, 2005), and others. This, in spite of the fact that the transformational approach is intimately related to and even overlaps with Tymozcko’s more overtly geometric approach. And while AGM has a great deal to say about voice-leading, and has the word “counterpoint” in its subtitle, it has little to say about counterpoint as such or about imitative forms, even though such forms obviously are generated by geometric operations (though, of course, not upon chords, but upon sequences; viewing such sequences through the prism of chord space might be a fruitful topic for future research).

In his conclusion, Tymoczko writes “my initial goal in writing this book was to explore basic theoretical and compositional issues,” but as his writing progressed, he found that the “five features could also provide a helpful framework for understanding the development of Western music.” Despite the gaps and spotty context, I definitely agree.

For composers, I think what is most salient about AGM is that the “moves” we commonly use to get from one chord to another show up as short, typical movements in chord space with clear motivations that take one chord, usually not far from the central axis of augmented chords, to another. The same is true of the “moves” we use to get from one key to another, or to mutate between one scale and another.
And what is salient for computer composers is that these movements are easily implemented in code. An algorithm that works in the orbifold for trichords will also work, simply by increasing the number of dimensions, in the higher-dimensional orbifolds for seventh chords, ninth chords, and so on, up to various complete scales. An algorithm that works for one equivalence class will also work for another equivalence class, simply by changing the function that glues equivalent points together.

It is very nice, as a composer, to find a new perspective from which to view the landscape of music. But, as an algorithmic composer, it is stunning to be presented with a toolkit that brings efficient voice-leading, Riemannian and neo-Riemannian transformations, scale theory, and more, so transparently into the engine room of algorithmic composition. Most importantly, the geometric approach makes it easy to turn analytical operations into generative ones because the mathematics is simple. Once the notions of equivalence class and quotient space have been assimilated, the rest is no more difficult than high-school algebra and basic group theory. And, operations implemented geometrically can be highly efficient. For example, automatically finding a counterpoint for a cantus firmus using the rules of Gradus ad Parnassum requires pages of code and exponential time, while doing it by looking up the nearest (by Euclidean distance) voicings of a series of two-voice consonant chords in a dictionary of such voicings requires a few dozen lines of code and logarithmic time.
Tymoczko hopes the geometric approach will help composers to further extend tonality. I, for one, am trying to do that, in the sense that I am using generative procedures based on neo-Riemannian moves in chord spaces to create sequences that are difficult to imagine and yet harmonically and contrapuntally well-formed. I advise other composers to investigate the potential of AGM for their own purposes.